广东专插本是专科生拿到全日制本科毕业证书和学位证书的途径。南粤优师小编给大家整理了广东专插本考试历年真题供广大考生参考。如有疑问可在线咨询老师。
广东省2013年普通高等学校本科插班生招生考试
《高等数学》
一、单项选择题(本大题共5小题,每小题3分,共15分。每小题只有一个选项符合题目要求)
( )1.已经三个数列{an}、{bn}和{cn}满足an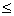 bn
bn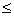 cn(n∈N+),且
cn(n∈N+),且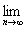 an=a,
an=a,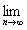 cn=c(a、b为常数,且a A.有界 B.无界 C.收敛 D.发散
cn=c(a、b为常数,且a A.有界 B.无界 C.收敛 D.发散
( )2.x=0是函数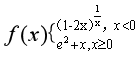 ,的
,的
A.连续点 B.可去间断点 C.跳跃间断点 D.第二类间断点
( )3.极限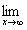 2xsin
2xsin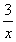 =
=
A.0 B.2 C.3 D.6
( )4.如果曲线y=ax-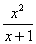 的水平渐近线存在,则常数a=
的水平渐近线存在,则常数a=
A.2 B.1C.0 D.-1
( )5.设f(x,y)为连续函数,将极坐标形式的二次积分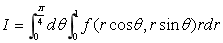 化为直角坐标形式,则I=
化为直角坐标形式,则I=
A.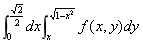
B.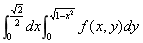
C.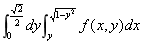
D.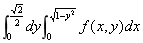
二、填空题(本大题共5小题,每小题3分,共15分)
6.设f(x)在点x0处可到,且f’(x0)=3,则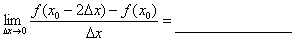
7.若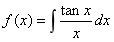 ,则f”(
,则f”(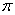 )=____ .
)=____ .
8.若曲线y=x3+ax2 +bx+1有拐点(-1,0),则常数b= ____.
9.广义积分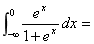 ________.
________.
10.设函数f(u)可微,且f’(o)=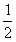 ,则z=f(4x2一y2)在点(1,2)处的全微分
,则z=f(4x2一y2)在点(1,2)处的全微分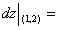 ______.
______.
三、计算题(本大题共8小题,每小题6分,共48分)
11.计算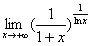 .
.
12.设函数y=f(x)由参数方程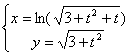 所确定,求
所确定,求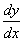
(结果要化为最简形式).
13.确定函数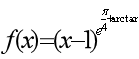 的单调区间和极值.
的单调区间和极值.
14.求不定积分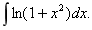 .
.
15.设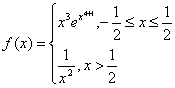 ,利用定积分的换元法求定积分
,利用定积分的换元法求定积分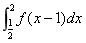 .
.
16.求微积分方程y’’一4y'+13y=0满足初始条件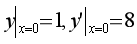 特解.
特解.
17.已知二元函数z=x(2y+1)x,求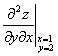 .
.
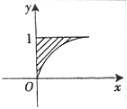
18.计算二重积分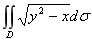 ,其中D是由曲线y=
,其中D是由曲线y=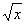 及直线y=1,x=0围成的闭区域.
及直线y=1,x=0围成的闭区域.
四、综合题(大题共2小题,第19小题12分,第20小题10分,共22分)
19.已知C经过点M(1,0),且曲线C上任意点P(x,y)(x≠0)处的切线斜率与直线OP(O为坐标原点)的斜率之差等于ax(常数a>0).
(1)求曲线C的方程;
(2)试确定a的值,使曲线C与直线y=ax围成的平面图形的面积等于 .
.
20.若当x→0,函数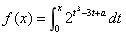 与x是等价无穷小量;
与x是等价无穷小量;
(1)求常数a的值;
(2)证明: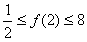 .
.
广东省2012年普通高等学校本科插班生招生考试
《高等数学》参考答案及评分标准
一、单项选择题(本大题共5小题,每小题3分,共15分)
1.A 2.C 3.D 4.B 5.C
二、填空题(本大题共5小题,每个空3分,共15分)
6.-6
7.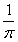
8.3
9.ln2
10.4dx - 2dy
三、计算题(本大题共8小题,每小题6分,共48分)
11.解:原式=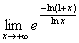 , (2分) .
, (2分) .
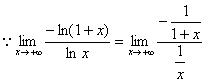 (4分)
(4分)
 (6分)
(6分)
12.解: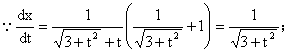
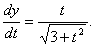 (3分)
(3分)
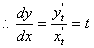 (结果没有化简扣2分). (6分)
(结果没有化简扣2分). (6分)
13.解:函数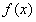 的定义域为
的定义域为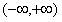 ,
,
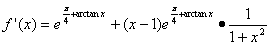
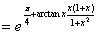 , (2分)
, (2分)
令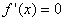 ,解得x=0,x=-1 因为在区间(-∞,-1)内,
,解得x=0,x=-1 因为在区间(-∞,-1)内,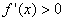 ;在区间(-l,0)内,
;在区间(-l,0)内,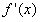 <0;
<0;
在区间(0,+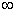 )内,
)内,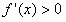 ,所以
,所以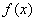
的递增区间是(-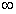 ,-1)及(0,+
,-1)及(0,+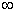 ),递减区间是(-1,0), (4分)
),递减区间是(-1,0), (4分)
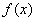 的极大值是
的极大值是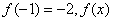 的极小值
的极小值 . (6分)
. (6分)
14.解: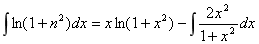 (2分),
(2分),
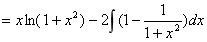
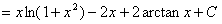 (6分)
(6分)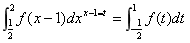 (2分)
(2分)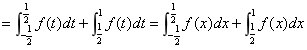
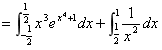 (4分)
(4分)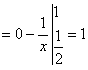 . (6分)
. (6分)16.解:由微分方程的特征方程r2 - 4r +13=0解得r=2±3i, (2分)
所以此微分方程的通解为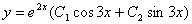 . (4分)
. (4分)
因为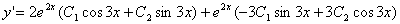 , 由
, 由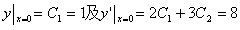
解得C1=1,C2=2,故所求特解为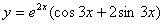 . (6分)
. (6分)
17.解: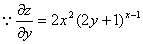 , (2分)
, (2分)
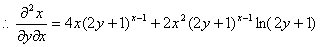 , (4分)
, (4分)
故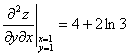 (6分)
(6分)
18.解:积分区域D如图:
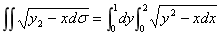 (3分)
(3分)
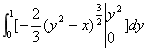
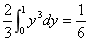
 (6分)
(6分)四、综合题(本大题共2小题,第19小题12分,第20小题10分,共22分)
19.解:(1)设曲线C的方程为y=厂O),由题意知
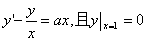 . (2分)
. (2分)
由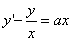 得
得
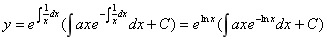 (4分)
(4分)
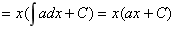 ,
,
因为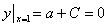 ,解得
,解得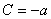
故曲线C的方程为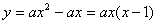 . (6分)
. (6分)
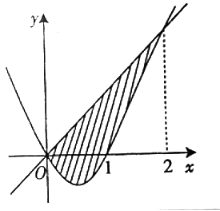
(2)如图,
由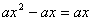 解得x=0,x=2, (10分)
解得x=0,x=2, (10分)
即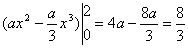 ,解得a=2. (12分)
,解得a=2. (12分)
由题意知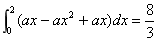 ,
,
20.解:(1)解:由题意知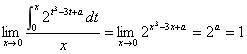 , (4分)
, (4分)
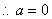 .
. (2)证: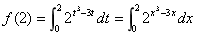 ,
,
设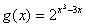 ,
,
则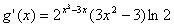 , (6分)
, (6分)
令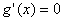 ,在区间(0,2)内解得x=l,
,在区间(0,2)内解得x=l,
因为g(0)=1,g(1)=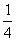 ,g(2)=4,
,g(2)=4,
所以g(x)在区间[0,2]上的最大值为4,最小值为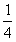 . (8分)
. (8分)
由定积分的估值定理可得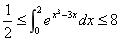 ,
,
所以有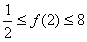 . (10分)
. (10分)
本文标题: 2012年广东专插本考试数学真题+答案
本文地址: https://zcb.huashi-edu.org.cn/index.php/article/shuxue/303.html













