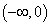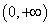广东专插本是专科生拿到全日制本科毕业证书和学位证书的途径。南粤优师小编给大家整理了广东专插本考试历年真题供广大考生参考。如有疑问可在线咨询老师。
广东省2011年普通高等学校本科插班生招生考试
《高等数学》真题
一、选择题(本大题共5题,每小题3分,共15分。每小题只有一个选项符合题目要求)
( )1.下列极限等式中,正确的是
A. 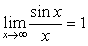
B.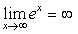
C. 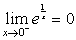
D.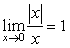
( )2.若函数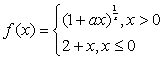 在
在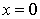 处连续,则常数a=
处连续,则常数a=
A.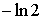
B.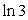
C.2
D.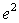
( )3.已知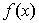 的二阶导数存在,且
的二阶导数存在,且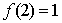 ,则
,则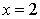 是函数
是函数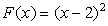 的
的
A. 极小值点
B. 最小值点
C. 极大值点
D. 最大值点
( )4.若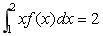 ,则
,则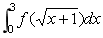 =
=
A.1 B.2 C.3 D.4
( )5.设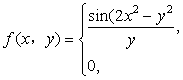
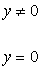 ,则
,则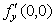 =
=
A.-1 B.0 C.1 D.2
二、填空题(本大题共5小题,每小题3分,共15分)
6 当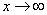 时,
时,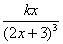 与
与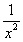 是等价无穷小,则常数k= .
是等价无穷小,则常数k= .
7 设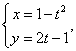 则
则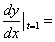 .
.
8 已知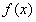 在
在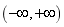 内连续,且
内连续,且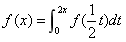 ,则
,则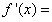 .
.
9 已知二元函数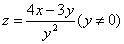 ,则
,则 .
.
10 设平面区域D由直线y=x,y=2x及x=1所围成,则二重积分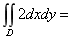 .
.
三、计算题(本大题共8小题,每小题6分,共48分)
11 计算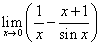 .
.
12 已知函数f(x)的n-2阶导数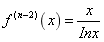 ,求
,求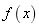 的n阶导数。
的n阶导数。
13 求曲线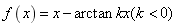 的凹凸区间和拐点。
的凹凸区间和拐点。
14 计算不定积分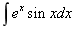
15 计算定积分
16 求微分方程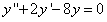 满足初始条件
满足初始条件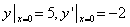 的特解。
的特解。
17 已知隐函数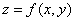 由方程
由方程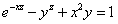 所确定,求
所确定,求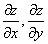
18 已知直角坐标系下二重积分: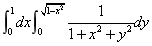 ,试用极坐标法计算二重积分。
,试用极坐标法计算二重积分。
四、综合题(本大题共2小题,第19题10分,第20题12分,共22分)
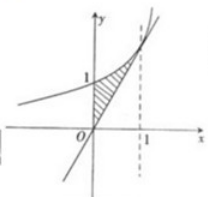
19 过坐标原点作曲线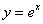 的切线l,切线l与曲线
的切线l,切线l与曲线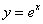 及y轴围成的平面图形记为G.求:
及y轴围成的平面图形记为G.求:
(1)切线l的方程;(2)G的面积;(3)G绕x轴旋转所得旋转体体积。
20 若定义在区间(0,π)的可导函数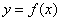 满足
满足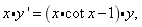 且
且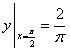 .求:
.求:
(1)函数y=f(x)的表达式;(2)证明:函数y=f(x)在区间(0,π)内单调递减。
广东省2011年普通高等学校本科插班生招生考试
《高等数学》参考答案及评分标准
一、单项选择题
1 C 2 B 3 C 4 D 5 A
二、填空题
6 .8 7. -1 8 .2f(x) 9 . 0 10.1
三、计算题
11 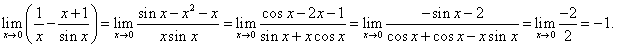
12 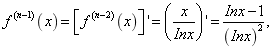
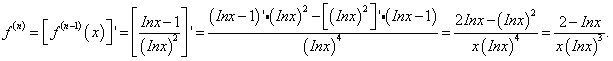
13 函数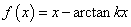 的定义域为
的定义域为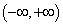 ;
;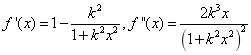
令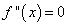 ,解得x=0,列表讨论如下(k<0):
,解得x=0,列表讨论如下(k<0):
x |
| 0 |
|
y’’ | + | 0 | - |
y | 凹 | 拐点 | 凸 |
拐点是(0,0),f(x)在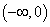 是凹的,在
是凹的,在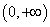 是凸的。
是凸的。
14 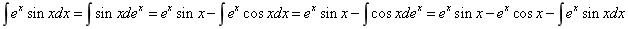
即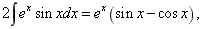
∴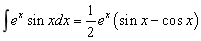
15 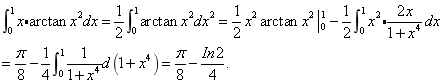
16 微分方程的特征方程为: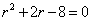 ;解得:r1=-4,r2=2,
;解得:r1=-4,r2=2,
∴微分方程的通解为: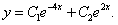
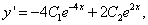
∴有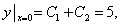
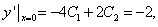 解之得:
解之得: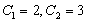 .
.
故特解为: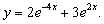
17 设F(x,y,z)=e-xz-yz+x2y-1,则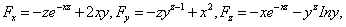
∴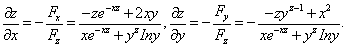
18 画出几分区域D,可知积分区域是在第一象限的四分之一圆,则:
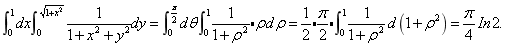
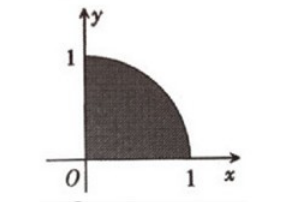
四、综合题
19 (1)设切点的坐标为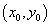 ,则
,则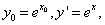
∴切线l的方程为: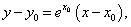 即
即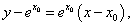 又因该切线经过原点,故
又因该切线经过原点,故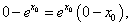 解之得
解之得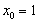 ,∴切点为
,∴切点为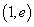 ,故切线方程为y=ex;
,故切线方程为y=ex;
(2)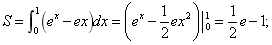
(3)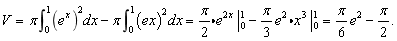
20 (1)由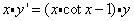 可得
可得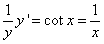 ,两边积分得:Iny=Insinx-Inx+C1,化简得
,两边积分得:Iny=Insinx-Inx+C1,化简得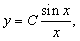 又
又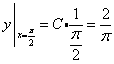 ,解之得C=1,
,解之得C=1,
∴函数y=f(x)的表达式为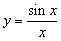 ;
;
(2)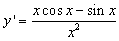 ,设g(x)=xcosx-sinx,
,设g(x)=xcosx-sinx, 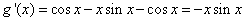 ,
,
因sinx在(0,π)区间内恒大于0,故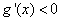 ,
,
∴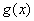 是单调减函数;
是单调减函数;
又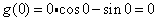 ,∴
,∴ 在区间(0,π)内恒小于0,
在区间(0,π)内恒小于0,
故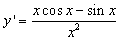 在区间(0,π)内恒为负,
在区间(0,π)内恒为负,
∴函数y=f(x)在区间(0,π)内单调递减。
本文标题: 2011年广东专插本考试数学真题+答案
本文地址: https://zcb.huashi-edu.org.cn/index.php/article/shuxue/302.html